Relación
Una relacion es un vinculo o una correspondencia. En el caso de la relación matemática, se trata de la correspondencia que existe entre dos conjuntos: a cada elemento del primer conjunto le corresponde al menos un elemento del segundo conjunto.
Cuando a cada elemento de un conjunto le corresponde solo uno del otro, se habla de función. Esto quiere decir que las funciones matemáticas siempre son, a su vez, relaciones matemáticas, pero que las relaciones no siempre son funciones.
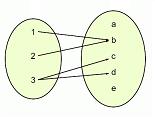
En una relación matemática, al primer conjunto se lo conoce como dominio, mientras que el segundo conjunto recibe el nombre de rango o recorrido. Las relaciones matemáticas existentes entre ellos se pueden graficar en el esquema llamado plano cartesiano.
Supongamos que el dominio se llama M y el rango, N. Una relación matemática de M en N sera un subconjunto del producto cartesiano M x N. Las relaciones, en otras palabras, serán pares ordenados que involucren elementos de M con elementos de N.
Si M = {5, 7} y N = {3, 6, 8}, el producto cartesiano de M x N serán los siguientes pares ordenados:
M x N ={5, 3), (5, 6), (5, 8), (7, 3), (7,6), (7, 8)}
Con este producto cartesiano, se pueden definir diferentes relaciones. La relación matemática del conjunto de pares cuyo segundo elemento es menor a 7 es R = {(5,3), (5, 6), (7,3), (7, 6)}
Otra relación matemática que puede definirse es aquella del conjunto de pares cuyo segundo elemento es para: R = {(5, 6), (5, 8), (7, 6), (7, 8)}
Las aplicaciones de las relaciones matemáticas trascienden los limites de la ciencia, ya que en nuestra vida cotidiana solemos hacer uso de sus principios, muchas veces de manera inconsciente. Seres humanos, edificios, electrodomésticos, películas y amigos, entre otros muchos, son algunos de los conjuntos mas comunes de interés para nuestra especie, y a diario establecemos relaciones entre ellos para organizarnos y participar de nuestras actividades.
De acuerdo con el numero de conjuntos que participen del producto cartesiano, es posible reconocer diversos tipos de relación matemática, algunos de los cuales se definen brevemente a continuación.
- Relación Unaria
- Relación Binaria
- Relación Ternaria
_________________________________________________________________________________
Función
Una funcion la denotamos por “f” es una relación entre un conjunto dado X (el dominio) y otro conjunto de elementos Y (el codominio) de forma que a cada elemento x del dominio le corresponde un único elemento del codominio f(x). Se denota por: f: X—-> Y
Comúnmente, el término función se utiliza cuando el codominio son valores numéricos, reales o complejos. Entonces se habla de función real o función compleja mientras que a las funciones entre conjuntos cualesquiera se las denomina aplicaciones.
Una función puede considerarse como un caso particular de una relación o de correspondencia matemática. Cada relación o correspondencia de un elemento x pertenece a X con un (y sólo un) y pertenece a Y se denota f(x)= y , en lugar de
(x,y) pertenece f.
Formalmente, pedimos que se cumplan las siguientes dos condiciones:
Condición de existencia: Todos los elementos de X están relacionados con elementos de Y.
Condición de unicidad: Cada elemento de X está relacionado con un único elemento de Y.
Clasificación de las funciones:
Dados dos conjuntos X, Y, consideremos a todas las posibles aplicaciones (funciones) que pueden formarse entre estos dos conjuntos. Podemos diferenciar los siguientes casos:
Si a cada imagen le corresponde una única preimagen, inyectiva.
Si la imagen de la función es igual al codominio, sobreyectiva o suprayectiva.
Una función que sea inyectiva y sobreyectiva simultáneamente, se denomina biyectiva .
Puede haber funciones que sean biyectivas, inyectivas pero no suprayectivas, supreyectiva pero no inyectiva o que no se cumple ninguna de esas condiciones, en cuyo caso no tiene un nombre específico.
Definiciones alternas: sea f: X —> Y dada y sea b un elemento cualquiera del codominio Y. Consideremos la ecuación:
f(x)= b (*).
La función es suprayectiva o sobreyectiva si, y sólo si, la ecuación (*) siempre tiene al menos una solución.
La función es inyectiva si, y sólo si, la ecuación (*) tiene a lo más una solución.
La función es biyectiva cuando, y sólo cuando, es inyectiva y suprayectiva a la vez.
Vamos a ilustrar esos diferentes tipos de funciones (aplicaciones) en un diagrama de venn, el conjunto universal U, representado por un rectángulo, es el conjunto de todas las posibles aplicaciones, el conjunto A es aquel de las aplicaciones inyectivas, y el conjunto B aquel de las sobreyectivas, esto nos permite ver los distintos tipos de aplicaciones de un modo gráfico.
_________________________________________________________________________________
Definición matemática de Relación y de Función
En matemática, Relación es la correspondencia de un primer conjunto, llamado Dominio , con un segundo conjunto, llamado Recorrido o Rango , de manera que a cada elemento del Dominio le corresponde uno o más elementos del Recorrido o Rango.
Por su parte, una Función es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del Recorrido.
De las definiciones anteriores podemos deducir que todas las funciones son relaciones , pero no todas las relaciones son funciones.
También debemos agregar que toda ecuación es una Relación , pero no toda ecuación es una Función.
Todas las Relaciones pueden ser graficadas en el Plano Cartesiano.
___________________________________________________________________________________
Funciones y Relaciones
SlideShare
_________________________________________________________________________________












0 comentarios:
Publicar un comentario