Conceptos Matemáticos
Revisión De Los Conceptos De Matemáticas Básicas De Uso Frecuente En Estadística
Para el correcto entendimiento de la teoría de los principios básicos estadísticos y poder manejar sus aplicaciones, se requiere del conocimiento de unos principios matemáticos y algebraicos. Revisaremos algunos algoritmos y tópicos de matemáticas de uso frecuente en estadística.
PROPIEDADES DE LA SUMA
La suma tiene cuatro propiedades. Las propiedades son conmutativa, asociativa, distributiva y elemento neutro.
- Propiedad Conmutativa Cuando se suman dos números, el resultado es el mismo independientemente del orden de los sumando. Por ejemplo 4+2 = 2+4
- Propiedad Asociativa Cuando se suman tres o más números, el resultado es el mismo independientemente del orden en que se suman los sumandos. Por ejemplo (2+3) + 4= 2 + (3+4)
- Elemento neutro La suma de cualquier número y cero es igual al número original. Por ejemplo 5 + 0 = 5.
- Propiedad distributiva La suma de dos números multiplicada por un tercer número es igual a la suma de cada sumando multiplicado por el tercer número. Por ejemplo 4 * (6+3) = 4*6 + 4*3
LA SUMATORIA Y SUS PROPIEDADES
La sumatoria o sumatorio se emplea para representar la suma de muchos o infinitos sumandos.
Fuente: Rodríguez, O. (2015) Generalidades Estadística.
La expresión se lee "sumatoria de Xi, donde i toma los valores de 1 a n". La operación sumatoria se expresa con la letra griega sigma mayúscula Σ.
- i es el valor inicial llamado limite inferior
- n es el valor final llamado limite superior
Si la sumatoria abarca la totalidad de los valores, su expresión se puede simplificar
Fuente: Rodríguez, O. (2015) Generalidades Estadística.
Es frecuente el uso del operador sumatoria en Estadística. La suma de las frecuencias absolutas se puede expresar como
Fuente: Rodríguez, O. (2015) Generalidades Estadística.
y la media como
Fuente: Rodríguez, O. (2015) Generalidades Estadística.
Fuente: Rodríguez, O. (2015) Generalidades Estadística.
PROPIEDADES DE LA SUMATORIA
La suma del producto de una constante por una variable, es igual a k veces la sumatoria de la variable.
Fuente: Rodríguez, O. (2015) Generalidades Estadística.
La sumatoria hasta N de una constante, es igual a N veces la constante.
Fuente: Rodríguez, O. (2015) Generalidades Estadística.
La sumatoria de una suma es igual a la suma de las sumatorias de cada término.
Fuente: Rodríguez, O. (2015) Generalidades Estadística.
La sumatoria de un producto no es igual al producto de las sumatorias de cada término.
Fuente: Rodríguez, O. (2015) Generalidades Estadística.
La sumatoria de los cuadrados de los valores de una variable no es igual a la sumatoria de la variable elevado al cuadrado.
Fuente: Rodríguez, O. (2015) Generalidades Estadística.
PLANO CARTESIANO
El plano cartesiano está formado por dos rectas numéricas perpendiculares, una horizontal y otra vertical que se cortan en un punto. La recta horizontal es llamada eje de las abscisas o de las equis (x), y la vertical, eje de las ordenadas o de las yes, (y); el punto donde se cortan recibe el nombre de origen.
Fuente: Rodríguez, O. (2015) Generalidades Estadística.
El plano cartesiano tiene como finalidad describir la posición de puntos, los cuales se representan por sus coordenadas o pares ordenados.
Cuando hablamos de par ordenado, nos estamos refiriendo a dos números, o figuras, encerrados en un paréntesis. Su representación general es (a , b)
Respecto a esto, podemos preguntarnos ¿cómo se obtiene un par ordenado?, ¿para qué sirve un par ordenado? Un par ordenado se puede obtener desarrollando una función o realizando la operación llamada producto cartesiano.
Como consecuencia, un par ordenado sirve para representar un subconjunto del producto cartesiano entre dos conjuntos, un punto en un plano cartesiano o bien una razón o una función.
Las coordenadas se forman asociando un valor del eje de las equis a uno de las yes, respectivamente, esto indica que un punto (P) se puede ubicar en el plano cartesiano tomando como base sus coordenadas, lo cual se representa como P (x , y)
Para localizar puntos en el plano cartesiano se debe llevar a cabo el siguiente procedimiento
- Para localizar la abscisa o valor de x, se cuentan las unidades correspondientes hacia la derecha si son positivas o hacia la izquierda si son negativas, a partir del punto de origen, en este caso el cero.
- Desde donde se localiza el valor de x, se cuentan las unidades correspondientes (en el eje de las ordenadas) hacia arriba si son positivas o hacia abajo, si son negativas y de esta forma se localiza cualquier punto dadas ambas coordenadas.
Ejemplo. Localizar el punto A (-4, 5) en el plano cartesiano.
El punto A se ubica 4 lugares hacia la izquierda en la abscisa (x) y 5 lugares hacia arriba en ordenada (y).
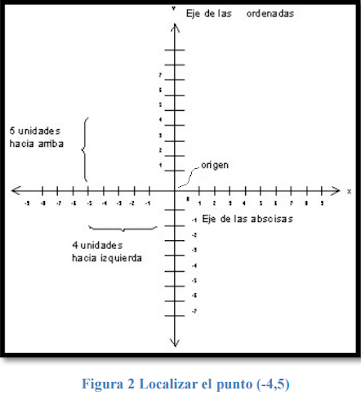
Fuente: Rodríguez, O. (2015) Generalidades Estadística.
FUNCION
Sean los conjuntos dados, X el uno y Y el otro, una función F de X hacia Y es una regla que asigna a cada elemento x del conjunto X un elemento y del conjunto Y y solo uno.
Lo anterior se expresa y = f(x), donde x es la variable dependiente y y es la variable independiente.
Ejemplo. Una empresa que ensambla equipos de cómputo contrata a un técnico especializado con un salario de $ 600,000 pesos mensuales más $ 80,000 por cada equipo armado que entregue a la empresa, de esta forma el salario del técnico es función de su producción y la ley de dependencia es
S = 600,000 + 80,000 x
En donde S es el salario (variable dependiente) y x es el número de equipos ensamblados (variable independiente).
Si en determinado mes el trabajador ensambló 32 equipos, el salario será
S = 600,000 + (80,000)(32) = 600,000 + 2,560,000 = 3,160,000
Funciones Lineales
Una función lineal es una función cuyo dominio son todos los números reales, cuyo codominio son también todos los números reales, y cuya expresión analítica es un polinomio de primer grado.
f: R ——-> R / f(x) = a.x+b donde a y b son números reales, es una función lineal.
Por ejemplo, son funciones lineales
- f: f(x) = 2x+5
- g: g(x) = -3x+7
- h: h(x) = 4
Nota: Las funciones lineales son polinomios de primer grado
Fuente: Rodríguez, O. (2015) Generalidades Estadística.
Recordemos que los polinomios de primer grado tienen la variable elevada al exponente 1. Es habitual no escribir el exponente cuando este es 1.
Ejemplos a(x) = 2x+7 b(x) = -4x+3 f(x) = 2x + 5 + 7x - 3
De estas funciones, vemos que la f no está reducida y ordenada como las demás. Podemos reducir términos semejantes para que la expresión quede de una forma mas sencilla, f(x) = 9x + 2
También recordemos que hemos convenido que cuando no establecemos en forma explícita el dominio y el codominio de una función, supondremos que es el mayor conjunto posible en cada caso.
Por ejemplo, si hablamos de la función f, de dominio real y codominio real, tal que f(x)= 2x-6, anotaremos f: R ——-> R / f(x) = 2x-6
Siendo el dominio todos los números reales, R, y el codominio también, todos los números reales, R.
Esto se lee " f de R en R tal que f de x es igual a 2x-6"
Vamos a graficar esta función, que tal cual lo vimos en la definición, es una función lineal por ser de primer grado. Para graficarla haremos una tabla de valores.
f: R ——> R / f(x) = 2x-6
Le vamos dando valores a "x". ¿Qué valores le podemos dar? Cualquiera que esté dentro del dominio. Por ejemplo, si x = 5, entonces f(x) pasa a ser f(5), que es f(5) = 2.(5)-6 f(5) = 4 Entonces al 5 le corresponde el 4. Nuestro punto es el (5,4).
Una función lineal cumple además, que el incremento de los valores de los elementos del dominio es proporcional al incremento de los valores en el codominio, siempre que a no sea cero.
Este número a se llama pendiente o coeficiente angular de la recta.
Volvamos a esto ejemplos de funciones lineales
f: f(x) = 2x+5
- si x es 3, entonces f(3) = 2(3)+5 = 11
- si x es 4, entonces f(4) = 2(4)+5 = 13
- si x es 5, entonces f(5) = 2(5)+5 = 15
Cada vez que la x se incrementa en 1 unidad, el resultado, esto es, f(x), se incrementa en 2 unidades. Preste atención en que los valores de x y de f(x) no son proporcionales. Lo que son proporcionales son los incrementos.
g: g(x) = -3x+7
- si x= 0, entonces g(0) = -3(0)+7 = 0+7 = 7
- si x= 1, entonces g(1) = -3(1)+7 = -3+7 = 4
- si x= 2, entonces g(2) = -3(2)+7 = -6+7 = 1
Cada vez que la x se incrementa en 1 unidad, el resultado, esto es, g(x), disminuye en 3 unidades.
h: h(x) = 4
- si x= 0, entonces h(0) = 4
- si x= 9, entonces h(9) = 4
Cada vez que la x se incrementa en 1 unidad, el resultado, esto es, h(x), NO aumenta. Es la función constante. Su gráfica es una recta paralela al eje OX.
Fuente: Rodríguez, O. (2015) Generalidades Estadística.
¿Qué diferencia fundamental y muy importante hay entre las funciones h y j?
Parecería, a primera vista, que son muy parecidas. Las "fórmulas" de ambas son iguales h(x) = 3 y j(x)=3. Sin embargo, son muy distintas porque mientras la función h tiene como dominio todos los números reales, la función j tiene como dominio los números naturales. Y como entre dos números naturales consecutivos no hay ningún otro número natural, no existe gráfica ni puntos entre ellos.
Esto es, entre el 17 y el 18 no hay ningún número natural. Entre el 17 y el 18 hay infinitos número reales. He ahí la diferencia. La representación gráfica de h es una línea recta, pero la de j son puntos aislados, aunque son infinitos.
RESUMEN
Las funciones lineales son funciones de dominio real y codominio real, cuya expresión analítica es
f: R —> R / f(x) = a.x+b
La representación gráfica de dichas funciones es una recta, en un sistema de ejes perpendiculares. La inclinación de dicha recta está dada por la pendiente a y la ordenada en el origen es b.con a y b números reales.
Bibliografía
- Rodríguez, O. (2015). Estadística Y Probabilidad, Generalidades Estadística. Armenia, Quindio, Ciencias Administrativas Y Financieras. Campus Virtual EAM

























0 comentarios:
Publicar un comentario